Principe de minimisation du risque empirique Principe dans lequel on se donne une classe de fonctions \(\mathcal S\) et on construit \(\hat g_l\) comme la fonction dans \(\mathcal S\) qui minimise le Risque empirique sur l'échantillon \((X_1,Y_1),\dots,(X_l,Y_l)\). $$\hat R_l(\hat g_l)=\min_{g\in\mathcal S}\underbrace{\frac1l\sum^l_{i=1}\rho(Y_i,g(X_i))}_{=:\,\hat R_l(g)}$$

• la difficulté de cette approche est que \(\hat g_l\) est choisie pour minimiser le Risque empirique, et non le Risque effectif
    
• on dit que le principe de minimisation du risque empirique est consistant sur la classe \(\mathcal S\) si pour toute loi possible \(Q\) de \((X,Y)\), on a la Convergence en probabilité : $$R(\hat g_l)\overset Q{\underset{l\to+\infty}\longrightarrow}\min_{g\in\mathcal S}R(g)$$
        
• on a la consistance si \(\forall\varepsilon\gt 0\), \({\Bbb P}(\sup_{g\in\mathcal S}R(g)-\hat R_l(g)\ge\varepsilon)\underset{l\to+\infty}\longrightarrow0\)
• \(\mathcal S\) doit être assez grand pour avoir une faible Erreur d'approximation, mais assez petit pour avoir une faible Erreur de généralisation (compromis)

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Que se passe-t-il si l'écart \(\hat R_l(\hat g_l)-R(\hat g_l)\) entre le Risque empirique et le Risque effectif est trop grand ?
Verso: La machine fonctionne bien sur les données d'apprentissage, mais ne fonctionne pas bien sur des données qu'elle n'a jamais vues. Elle généralise mal.
Bonus:

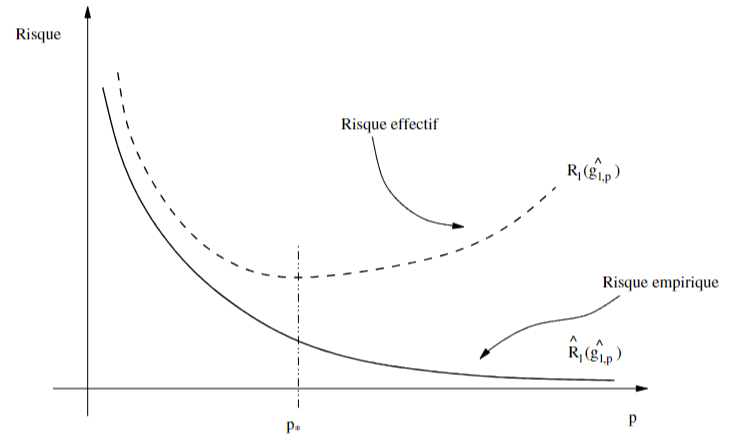Erreur de généralisation Carte inversée ?:
END